Overview
Neutron stars are among the most compact objects in the universe, reaching densities that are unreachable on Earth. Our understanding of the physics behind what causes these immense densities is limited and models which we produce are constructed using an equation of state (EoS). This project aims to link the microscopic and macroscopic properties of these compact stars using a hybrid EoS, where a phase transition from hadronic to quark matter occurs, to attain an understanding of how quark deconfinement within such stars could leave detectable signatures in gravitational-wave observations from binary mergers.
A Python implementation of a TOV solver (converted from Fortran) was used to generate mass–radius and tidal-deformability sequences for a set of hybrid EoS models. These results were compared against constraints consistent with GW170817.
Hybrid Equations of State and Phase Transition
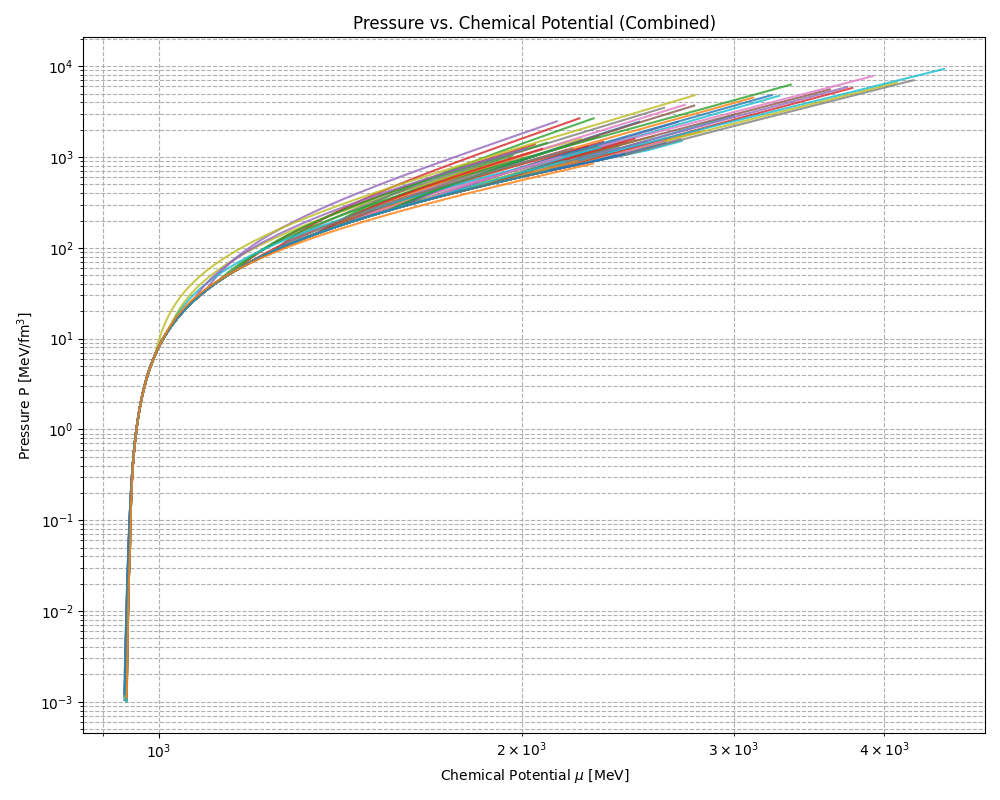
The pressure–chemical potential (P–μ) relation provides a clear thermodynamic view of the transition between the hadronic and quark phases. The intersection in a plot of pressure against chemical potential between the hadronic and quark branches marks the point of the phase transition. At pressures below this phase transition, the matter is hadronic. Once the phase transition occurs and the pressure rises beyond the transition point, the matter transitions to a deconfined quark phase. The pressure at which the phase transition occurs is dependent on the parameters of the EoS model, particularly the effective gluon mass.
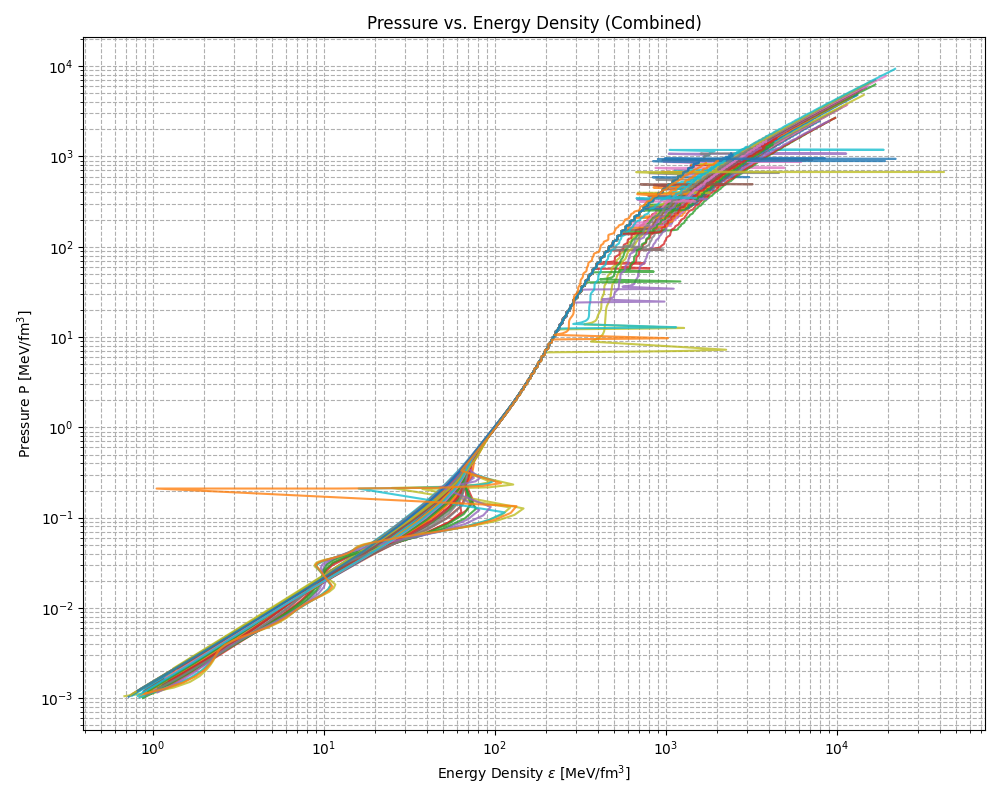
The pressure–energy density (P–ε) relation defines the macroscopic stiffness of matter and governs the overall structure and stability of compact stars. For hadronic matter, the pressure increases steadily with energy density, reflecting the growing resistance to compression. As the phase transition to quark matter begins, the curve softens— its slope decreases—indicating a temporary loss of stiffness. When the transition is strong, this discontinuity can produce an unstable region in the mass–radius sequence, eventually leading to the formation of a re-stabilised hybrid branch. This so-called twin-star behaviour illustrates how small changes in the microphysics of the equation of state can give rise to two classes of stars with similar masses but markedly different radii.
TOV Modelling, Twin-Star Behaviour and Mass–Radius Sequences
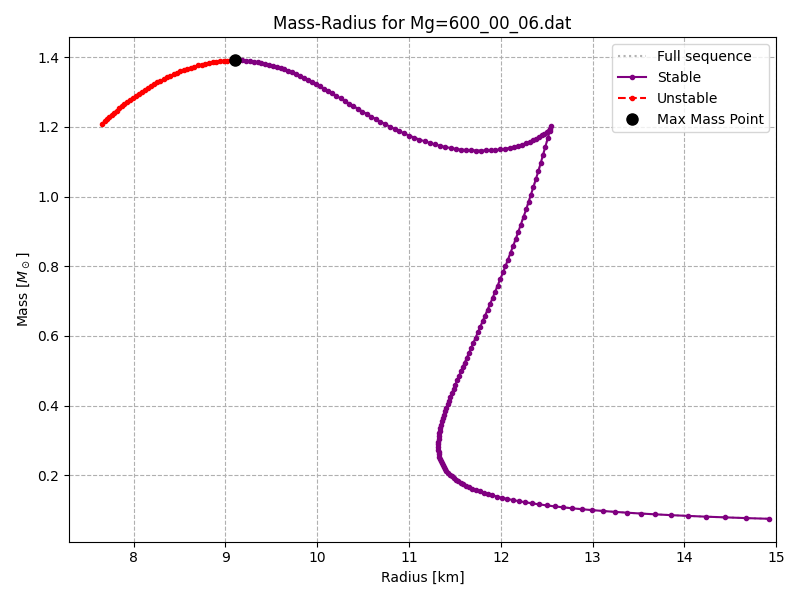
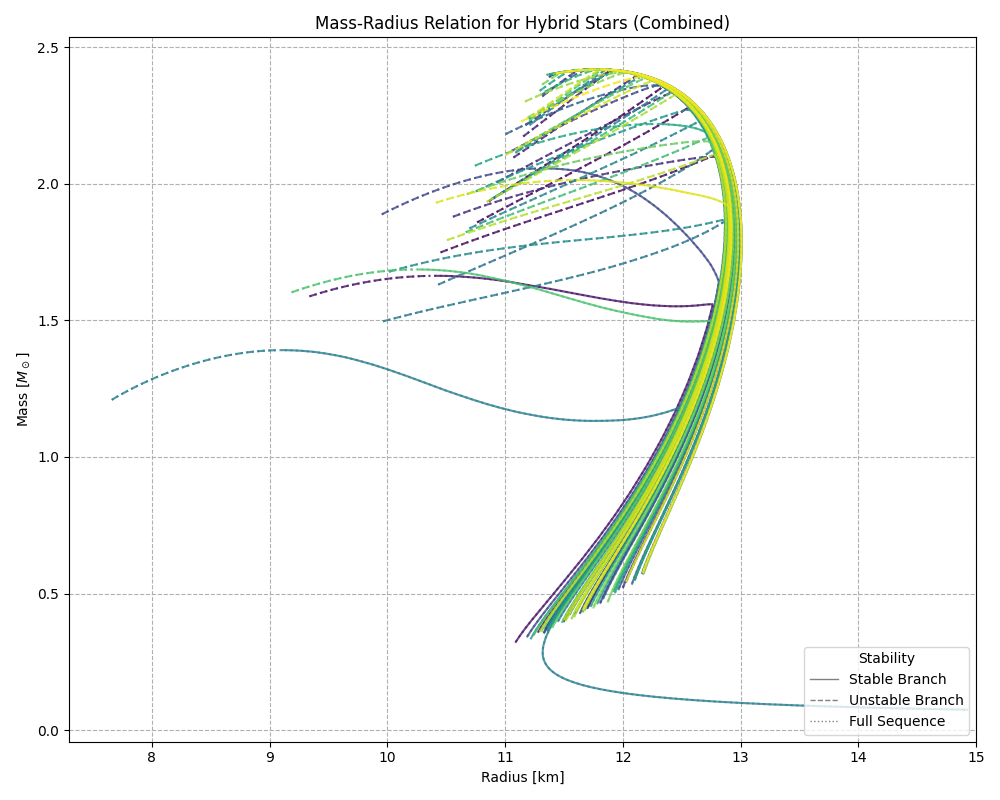
Integration of the Tolman–Oppenheimer–Volkoff (TOV) equations was performed for each EoS to obtain equilibrium sequences of mass and radius. The resulting plot indicates a strong first-order phase transition: a stable hadronic branch, a stable hybrid branch and an unstable hybrid branch. The existence of this stable hybrid branch indicates the possibility of a "twin-star" phenomenon, where two neutron stars can exist with the same mass but different radii.
In the generated models, the onset of instability corresponds to the softening visible in the pressure–energy density relation, while re-stabilisation coincides with the quark-matter branch becoming sufficiently stiff. The mass–radius diagram therefore encodes the entire transition sequence, providing direct visual evidence of the hybrid star phenomenon that underlies potential multi-branch populations detectable by next-generation gravitational-wave observatories.
Tidal Deformability
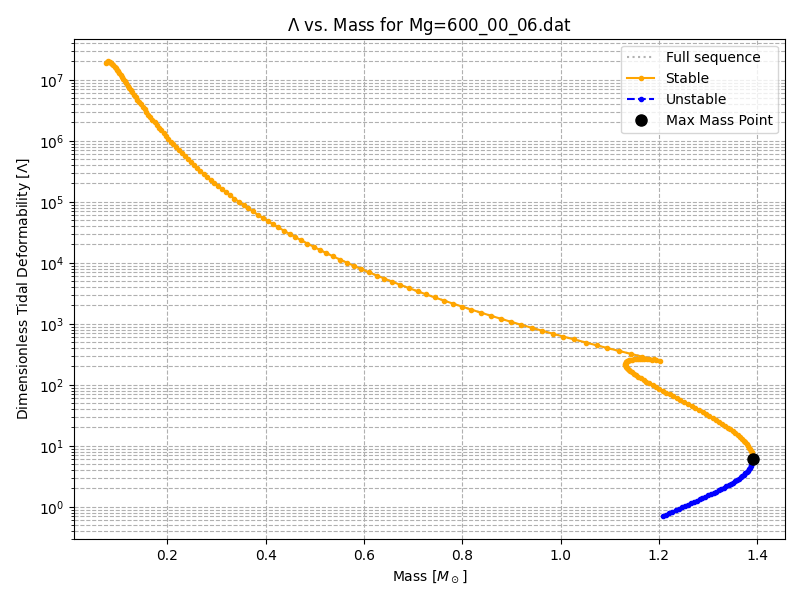
The tidal deformability (Λ) acts as the critical observable linking microscopic matter properties to the gravitational-wave signatures detected during binary neutron-star mergers. For a binary star system, as the two stars orbit each other, they emit gravitational waves. For neutron stars with higher tidal deformability, the tidal imprint on the gravitational-wave signal is stronger. As the star becomes more compact, Λ falls sharply—reducing the tidal imprint on the waveform. This behaviour, captured in the Λ–M relation, is particularly sensitive to the presence of a quark-matter core: once deconfinement occurs, the reduced internal stiffness drives a visible kink in the sequence, providing an indirect but measurable indicator of the phase transition.
For hybrid EoS models, this transition region produces a striking signature—an abrupt drop in Λ around the mass range corresponding to the hybrid branch in the M–R diagram. Within the context of GW170817 and the sensitivity of upcoming observatories such as the Einstein Telescope, this feature defines an astrophysical “hook”: a testable prediction that the imprint of quark deconfinement could emerge directly in the tidal phase evolution of binary inspirals. Thus, the tidal deformability is not only a measure of compactness but a probe of the fundamental structure of matter at supranuclear densities.
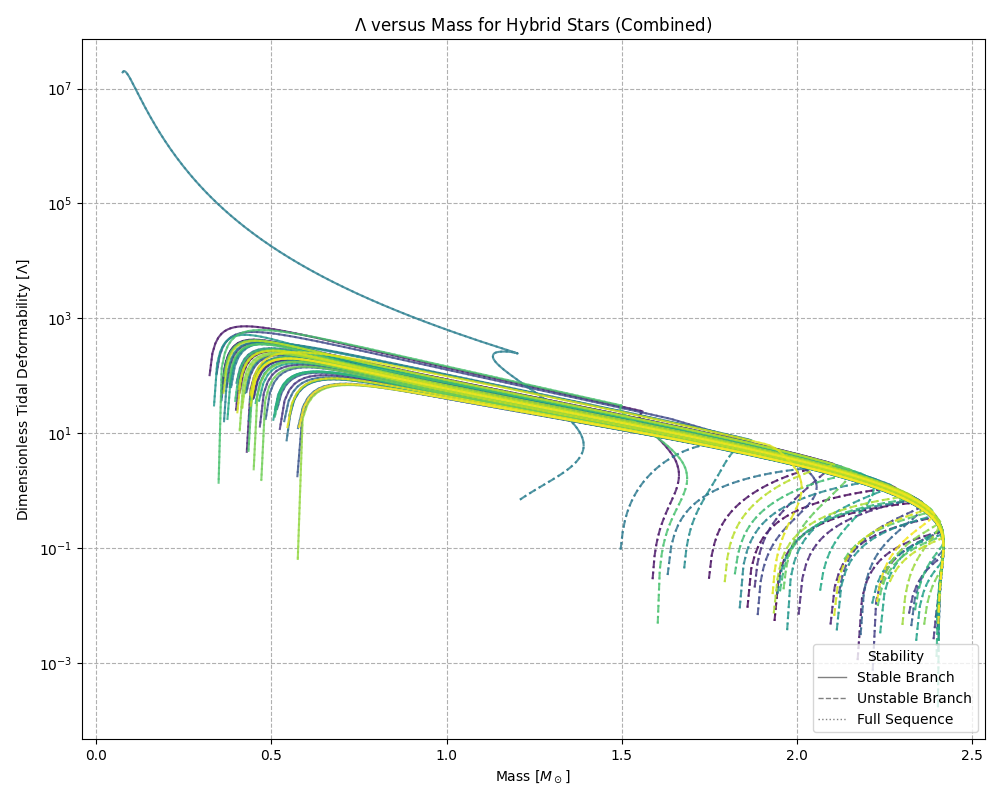
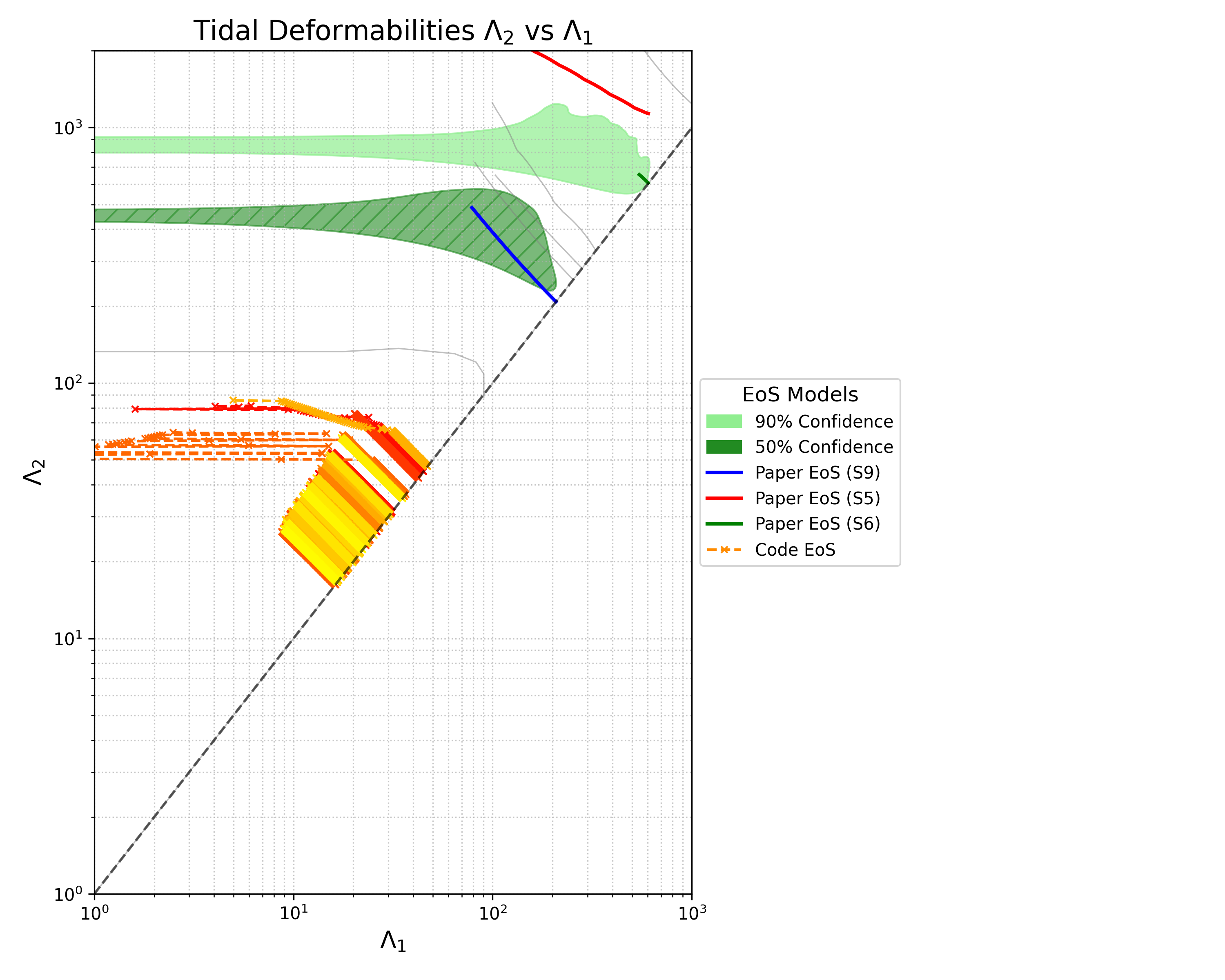
Summary
This project managed to model neutron stars from equations of state using a TOV solver, producing both Mass–Radius and Mass–Tidal Deformability plots. The data from these plots were then checked against observed constraints from published data.